In this video, Dr. Anthony Fesmire discusses how to create a 12 tone matrix from a twelve tone row. Video Text
Tonal music is organized by the relationships between chords in keys. The most important relationship being between the tonic and dominant chords with the tension created by the dominant and the resolution created by the movement from dominant to tonic. In an attempt to find a system for organizing atonal music, Arnold Schoenberg created serial music.
In this video, we will discuss twelve-tone serial music as developed by Arnold Schoenberg. In this type of composition, there is an attempt to make each note of equal importance; with each note being equal, there is no tonic. To do this, the composition is based on a 12 tone row that includes each of the notes of the chromatic scale. Here is a twelve tone row. Notice that each of the notes of the chromatic scale are included without repetition. For this example, I have used flats for some notes and sharps for others; this is only out of preference. Since all of the notes are of equal importance, C# or Db, for example, represent the same function and are, therefore, equivalent. Based on Schoenberg’s rules, a 12 tone row can be used in various ways within a composition.
1. The row can be transposed to start on any note of the chromatic scale
2. The original form and its transpositions can be used in inversion
3. The original form and its transpositions can be used in retrograde
4. The original form and its transpositions can be used in retrograde-inversion
By taking all of these possible versions of the 12 tone row, there are 48, a composer has a wealth of note choices to draw from in creating a composition. Schoenberg created the 12 tone matrix to organize the original row and all it derivations.
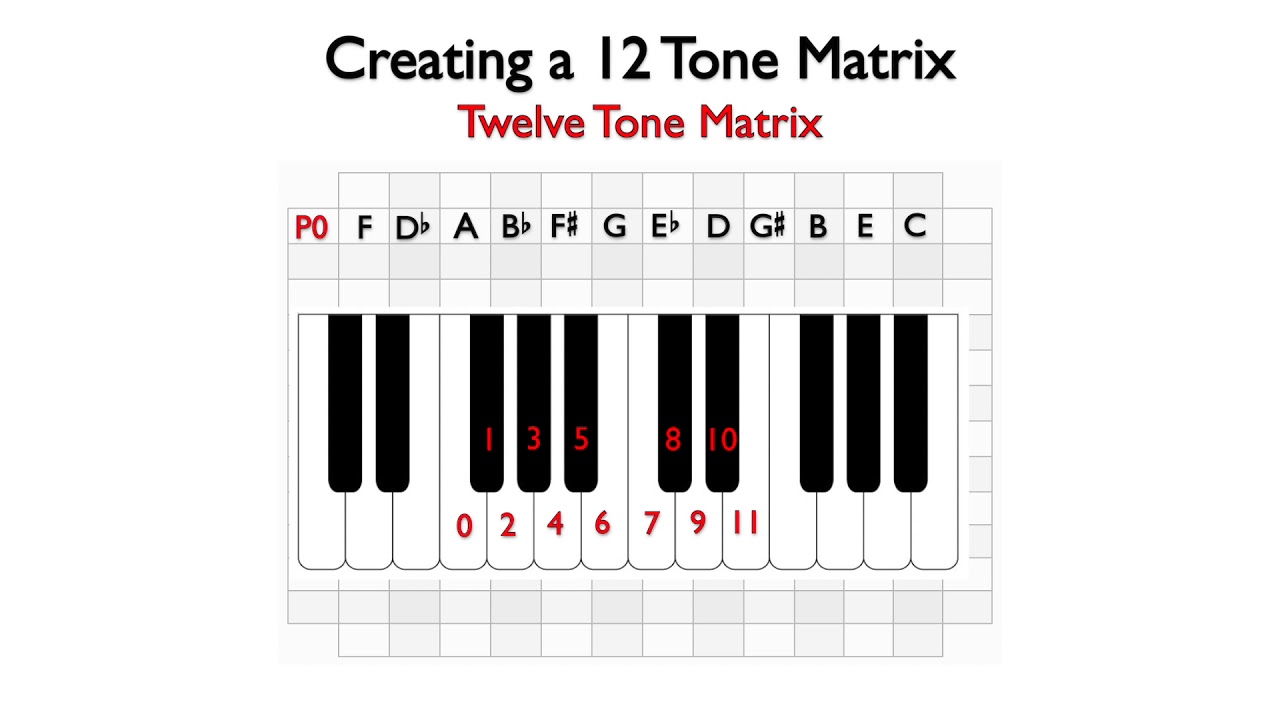
Here is a 12 tone matrix with only the original row included. This row will always be presented first in a composition, and is referred to as the Prime 0. Since our row begins on F, we will call it P0, with 0 representing the F note. On the piano, we will find the numbers for each note of the chromatic scale by numbering the half steps beginning on F...0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11. These numbers will be used to help name the other versions of the row.
Next, we will start on F and create the inversion. This will be referred to as I0 for the inversion beginning on the F note. In the prime form, F to Db is a minor 6 up; to invert, we will need to go down by a minor 6 from F to A. Db to A in the prime form is four half steps or the equivalent of a major third down. To invert this, we will go up by a major third from A to C#. A to Bb in the prime form is a half step up. In the inverted form, we will need to go down by a half step from C# to C. If we continue to invert the intervals, we will have the following for I0.
To complete the matrix, we would next need to create the transpositions of the prime form by using each of the notes of the inversion as a starting point. First, we will number the beginning note of each of the transposed prime forms. Since F is 0, F#/Gb is 1, G is 2, G#/Ab is 3, A is 4, Bb/A# is 5, B is 6, C is 7, C#/Db is 8, D is 9, D#/Eb is 10, and E is 11. Let’s begin by transposing P1: since it is only a half step from P0, it will be fairly easy to transpose. The note a half step above F is Gb or F#. I will use flats to simplify, but you could use sharps or a combination of both. The note a half step above Db is D; the note a half step above A is Bb; and we can work our way through the remainder of the notes of P0 to find the notes for P1 that are up by a half step. Next, we can move to P2 and find the notes by finding each of the notes that are a half step above the notes of P1. If we continue in this manner, we would next find the notes of P3 as up a half step from the notes of P2. Using this system, we can gradually find all of the notes for the 12 tone matrix based on our original 12 tone row. Here we have the 48 possible versions of our row. The transposed versions represented by P for prime. The retrograde versions represented by R. The inverted versions represented by I, and the retrograde of the inversions represented by RI.
0 Comments